[PART 4] WBBSE Class 8 Math Model Activity Task 2021 | অষ্টম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক উত্তরমালা

 

 

প্রিয় ছাত্রছাত্রীরা, এসো শিখিতে তোমাদের স্বাগত জানাই | এবছর আবার দেওয়া হলো বাংলার শিক্ষা পোর্টাল থেকে বিভিন্ন শ্রেনীর মডেল অ্যাক্টিভিটি টাস্ক |

আজকের এই পোস্টে আমরা আলোচনা করব পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের তরফ থেকে দেওয়া অষ্টম শ্রেনীর গণিত এর 2021 এর মডেল অ্যাক্টিভিটি টাস্ক এর উত্তরগুলি | আশা করি এতে তোমরা উপকৃত হবে | ( Class 8 Model Activity Task Mathematics 2021)

WBBSE Model Activity Task 2021

Class 8

গণিত (Math)

 Part 4

 

 নীচের প্রশ্নগুলির উত্তর লেখো :

1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs)

 

(i) $\small -\frac{2}{3}$ একটি

(a) অখন্ড সংখ্যা (b) ঋণাত্মক পূর্ণসংখ্যা (c) মূলদ সংখ্যা (d) স্বাভাবিক সংখ্যা

উত্তর: (c) মূলদ সংখ্যা

 

(ii) চিত্রে, আয়তক্ষেত্রাকার জায়গাটির দৈর্ঘ্য এবং প্রস্থের পরিমাপ থেকে ক্ষেত্রফলের পরিমাপে রাশিটির x -এর সহগ হলো

(a) 2 (b) 1 (c) −6 (d) −3

উত্তর: (d) − 3

ব্যাখ্যা: আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ

$\small =(2x^{2}+x)\times (x-3)$ 

$\small =2x^{3}-6x^{2}+x^{2}-3x$ 

$\small =2x^{3}-5x^{2}-3x$  

উপরিউক্ত সমাধান থেকে আমরা দেখতে পাচ্ছি যে x এর সহগ − 3

 

(iii) নীচের প্রতি জোড়া সম্পর্কগুলির মধ্যে সঠিক জোড়া সম্পর্কটি হলো (যেখানে a ও b মূলদ সংখ্যা এবং a ≠ 0, b ≠ 0)

(a) a + b = b + a, a − b = b − a

(b) a × b = b × a, a ÷ b = b ÷ a

(c) a + b = b + a, a ÷ b = b ÷ a

(d) a ÷ b ≠ b ÷ a, a − b ≠ b − a

উত্তর: (d) a ÷ b ≠ b ÷ a, a − b ≠ b − a

2. সত্য / মিথ্যা লেখো :

(i) একটি ঘনকের দৈর্ঘ্য y মিটার হলে, উহার আয়তন হবে 3y ঘনমিটার

উত্তর: মিথ্যা |

ব্যাখ্যা: ঘনকের আয়তন = (বাহুর দৈর্ঘ্য)³ = y³

(ii) চিত্রে $\small OA\bot OB $ এবং $\small \angle AOB$ -কে সমদ্বিখন্ডিত করলে যে দুটি কোণ উৎপন্ন হয় তারা পরস্পরের পূরক কোণ |

উত্তর: সত্য |

ব্যাখ্যা :

চিত্রে, ∵ $\small OA\bot OB $

∴  $\small \angle AOB = 90^{\circ}$

তাই, $\small \angle AOB$ কে সমদ্বিখন্ডিত করলে যে কোণ দুটি উৎপন্ন হবে তাদের সমষ্টি 90° হবে |

∴ $\small \angle AOB$ -কে সমদ্বিখন্ডিত করলে যে দুটি কোণ উৎপন্ন হয় তারা পরস্পরের পূরক কোণ - উক্তিটি সত্য |

(iii) একটি সরলরেখার বাইরের কোনো বিন্দু দিয়ে ওই সরলরেখার সমান্তরাল অসংখ্য সরলরেখা আঁকা যায় |

উত্তর: সত্য |

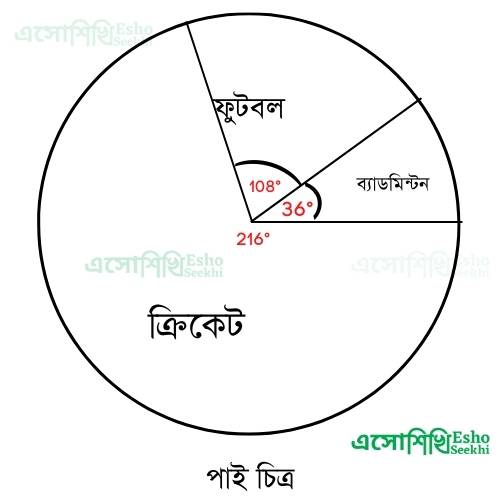
3. ক্লাসের ছাত্রছাত্রীরা কোন কোন খেলা কতজন করে পছন্দ করে শতকরায় তার তালিকা হলো  (একজন কেবলমাত্র একটি খেলায় পছন্দ করবে )

খেলা	খেলা পছন্দ করা ছাত্রছাত্রীর সংখ্যা (শতকরায়)
ক্রিকেট	60
ফুটবল	30
ব্যাডমিন্টন	10

পাই চিত্রে, যে বৃত্তকলাগুলি তথ্যটির অংশগুলিকে বোঝাবে সেই বৃত্তকলাগুলির কেন্দ্রীয় কোণগুলি নির্ণয় করো এবং তথ্যটির পাই চিত্র অঙ্কন করো |

সমাধান:

খেলা	খেলা পছন্দ করা ছাত্রছাত্রীর সংখ্যা (শতকরায়)	খেলা পছন্দ করা ছাত্রছাত্রীর সংখ্যা (ভগ্নাংশে)	কেন্দ্রীয় কোণের মান
ক্রিকেট	60	$\small \frac{\overset{3}{\not{6}\not{0}}}{\underset{5}{\not{1}\not{0}\not{0}}} = \frac{3}{5}$	$\small \overset{72}{\not{3} \not{6} \not{0}}\times \frac{3}{\not{5}} = 216^{\circ}$
ফুটবল	30	$\small \frac{3\not{0}}{1\thinspace 0 \thinspace \not{0}} = \frac{3}{10}$	$\small 3\thinspace \thinspace 6\not{0}\times \frac{3}{1\not{0}} = 108^{\circ}$
ব্যাডমিন্টন	10	$\small \frac{1\not{0}}{1\thinspace 0 \thinspace \not{0}} = \frac{1}{10}$	$\small 3\thinspace \thinspace 6\not{0}\times \frac{1}{1\not{0}} = 36^{\circ}$

 

∴ উপরের তথ্য গুলিকে পাই চিত্রের সাহায্যে প্রকাশ করলে হয়,

4.(i) $\small \frac{x}{2}=\frac{1}{2x}+1$ হলে, $\small \left ( x^{3}-\frac{1}{x^{3}} \right )$ এর মান নির্ণয় করো |

সমাধান: $\small \frac{x}{2}=\frac{1}{2x}+1$

 

বা, $\small \frac{x}{2}-\frac{1}{2x}=1$

 

উভয়পক্ষকে 2 দ্বারা গুন করে পাই,

বা, $\small \not{2} \times \frac{x}{\not{2}}-\not{2} \times \frac{1}{\not{2}x}=1$

বা, $\small x-\frac{1}{x}=2$

উভয়পক্ষে ঘন করে পাই,

$\small \left (x-\frac{1}{x}  \right )^{3}=(2)^{3}$

 

বা, $\small (x)^{3}-\left ( \frac{1}{x} \right )^{3}-3\cdot \not{x}\cdot \frac{1}{\not{x}}\left (x-\frac{1}{x}  \right )$

বা, $\small x^{3}-\frac{1}{x^{3}}-3\cdot 1 \cdot 2 = 8$

বা, $\small x^{3}-\frac{1}{x^{3}}-6 = 8$

বা, $\small x^{3}-\frac{1}{x^{3}}= 8+6$

∴ $\small x^{3}-\frac{1}{x^{3}}= 14$ (উত্তর)

 

(ii) ভাগ করো : $\small (m^{2}-5m+6)$ কে, $\small (m-3)$ দিয়ে |

সমাধান: 

$\small (m-3)$ ) $\small m^{2}-5m+6$ ( m − 2

                 $\small m^{2}-3m$

              −      +                                   

                        − 2m + 6

                        − 2m + 6

                         +       −                           

                          0

∴ নির্ণেয় ভাগফল = (m − 2) (উত্তর)

 

---

  আশা করি তোমরা উত্তরগুলি নিজেদের খাতায় টুকে নিয়েছ | আমাদের দ্বারা প্রকাশিত মডেল টাস্ক এর উত্তরগুলি ভালো লেগেথাকলে আমাদের ফেসবুক পেজ লাইক করে রাখতে পারো এবং আমাদের youtube চ্যানেল সাবস্ক্রাইব করে রাখতে পারো | নিচে দেওয়া লিংক থেকে Facebook YouTube জয়েন করো |

• Esho Seekhi Facebok
• Esho Seekhi YouTube

 

READ ALSO

 

এছাড়া তোমাদের আরও কোনো প্রশ্ন থাকলে নিচে কমেন্ট করে আমাদের জানাতে পারো অথবা আমাদের ফেসবুকে অথবা টেলিগ্রামে মেসেজ করতে পারো |

আমাদের টেলিগ্রাম গ্রুপে জয়েন হতে পাশের লিঙ্কে ক্লিক করুন : Telegram

এছাড়া আমাদের ফেসবুক পেজেও প্রশ্নের ছবি তুলে পাঠাতে পারো | আমাদের ফেসবুক পেজ জয়েন করার জন্য পাশের লিংকটিতে ক্লিক করো 👉 Esho Seekhi Facebook

 

Tags: model activity task 2021 class 8 all subject, class 8 model activity task 2021, model activity task class 8 math 2021, model activity task class 8 math answers, model activity task class 8 math, model activity task class 8 math part 4 answers, WBBSE Class 8 Math Model Activity Task Answers, Class 8 Model Activity Task Answers Math 2021, অষ্টম শ্রেণী অঙ্ক মডেল অ্যাক্টিভিটি টাস্ক উত্তরমালা 2021