[FINAL] WBBSE Class 7 Math Model Activity Compilation Part 8 Answers | সপ্তম শ্রেণী গণিত মডেল অ্যাক্টিভিটি পার্ট 8 সমাধান

 

প্রিয় ছাত্রছাত্রীরা, এসো শিখিতে তোমাদের স্বাগত জানাই | আজকের এই পোস্টে আমরা আলোচনা করব পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের তরফ থেকে দেওয়া সপ্তম শ্রেনীর গণিত এর 2021 এর মডেল অ্যাক্টিভিটি টাস্ক  Compilation এর উত্তরগুলি | আশা করি এতে তোমরা উপকৃত হবে | (Class 7 Model Activity Task Compilation Mathematics 2021 PART 8 Solutions)

Class 7

MODEL ACTIVITY COMPILATION

FINAL

গণিত

পূর্ণমান = 50

নীচের প্রশ্নগুলির উত্তর লেখো:

1. বহুমুখী উত্তরধর্মী প্রশ্ন:    1 × 8 = 8

(i) কোনটি ত্রিভুজের সর্বসমতার শর্ত নয়

(a) বাহু-বাহু-বাহু  (b) বাহু-কোণ-বাহু  (c) কোণ-কোণ-বাহু  (d) কোণ-কোণ-কোণ

উত্তর: (d) কোণ-কোণ-কোণ

(ii)$\small \frac{4}{49}$ বর্গসেমি ক্ষেত্রফল বিশিষ্ট বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য হবে 

 

(a) $\small \sqrt\frac{4}{49}$ (b) $\small \frac{2}{7}$ সেমি. (c) 2 সেমি. (d) 7 সেমি.

উত্তর: (b) $\small \frac{2}{7}$ সেমি.

ব্যাখ্যা: বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য হবে $\small= \sqrt{ \frac{4}{49}}$

(iii) 1.69 এর বর্গমূল হলো

(a) 13 (b) 1.3 (c) 0.13 (d) 13.03

উত্তর: (b) 1.3

ব্যাখ্যা: 1.69 এর বর্গমূল $\small \sqrt{1.69}$

$\small =\sqrt{\frac{169}{100}}$

$\small =\sqrt{\frac{13\times 13}{10\times10}}$

$\small =\frac{13}{10}$

$\small =1.3$

(iv) xy=

(a) $\small (x+y)^{2}-(x-y)^{2}$ (b) $\small (x+y)^{2}+(x-y)^{2}$

(c) $\small (\frac{x+y}{2})^2-(\frac{x-y}{2})^2$ (d) $\small (\frac{x+y}{2})^2+(\frac{x-y}{2})^2$

উত্তর: $\small (\frac{x+y}{2})^2-(\frac{x-y}{2})^2$

 

(v) যখন কোনো ট্রেন সেতু অতিক্রম করে তখন ট্রেনটিকে অতিক্রম করতে হবে −

(a) ট্রেনটির নিজের দৈর্ঘ্য     (b) সেতুর দৈর্ঘ্য 

(c) ট্রেনটির নিজের দৈর্ঘ্য + সেতুর দৈর্ঘ্য   (d) সেতুর দৈর্ঘ্য − ট্রেনটির নিজের দৈর্ঘ্য

উত্তর: (c) ট্রেনটির নিজের দৈর্ঘ্য + সেতুর দৈর্ঘ্য  

 

(vi) ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল =

(a) (বাহুর দৈর্ঘ্য)²     (b) বাহুগুলির দৈর্ঘ্যের সমষ্টি

(c) $\small \frac{1}{2}$(ভূমির দৈর্ঘ্য + উচ্চতা)  (d) $\small \frac{1}{2}$ভূমির দৈর্ঘ্য × উচ্চতা 

উত্তর: (d) $\small \frac{1}{2}$ভূমির দৈর্ঘ্য × উচ্চতা

 

(vii) $\small a^2-b^2$ =

(a) (a+b)²    (b) (a-b)²

(c) (a+b) (a-b)    (d) (a+b)² + (a-b)²

উত্তর: (a+b)(a-b)

 

(viii) রাস্তাসহ জমির দৈর্ঘ্য এবং রাস্তা বাদে জমির প্রস্থ হলো যথাক্রমে

(a) 23 মি., 21 মি. (b) 29 মি., 21 মি.

(c) 26 মি., 21 মি. (d) 26 মি., 15 মি.

উত্তর: (d) 26 মি., 15 মি.

2. সত্য/মিথ্যা লেখো (T/F):  1 × 8 = 8

(i) $\small (x+y)^2$ এর সূত্র থেকে $\small (x-y)^2$ এর সূত্র নির্ণয় করতে y এর পরিবর্তে (-y) লিখতে হবে।

উত্তর:   সত্য  

(ii) $\small (4-x)(x-4)=16-x^2$

উত্তর:   মিথ্যা  

(iii)

চিত্রে, $\small \angle 1$ ও $\small \angle 2$ পরস্পর অনুরূপ কোণ।

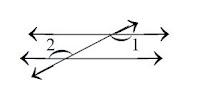
উত্তর:   মিথ্যা  

 

(iv) 

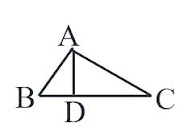
চিত্রে, বিষমবাহু $\small \Delta ABC$ এর একটি উচ্চতা AD। AD ত্রিভুজটির একটি মধ্যমা।

উত্তর:   মিথ্যা  

# মধ্যমা হলো কোনো ত্রিভুজের শীর্ষবিন্দু ও বিপরীত বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাংশ |

 

(v) দুটি স্তম্ভ চিত্রকে পাশাপাশি এঁকে দুটি তথ্য সহজে তুলনা করার জন্য যে চিত্র আঁকা হয় সেই চিত্রটি হলো দ্বিস্তম্ভ লেখ ।

উত্তর:   সত্য  

 

(vi) প্রথম ট্রেনের গতিবেগ x কিমি./ঘন্টা এবং দ্বিতীয় ট্রেনের গতিবেগ y কিমি./ঘন্টা । ট্রেন দুটি পরস্পর বিপরীত দিকে চললে 1 ঘন্টায় মোট যাবে (x-y) কিমি. ।

উত্তর:  মিথ্যা  

 

(vii)চিত্রে $\small \angle 1$ ও $\small \angle 2$ কোণ জোড়কে একান্তর কোণ বলা হয়।

উত্তর:  মিথ্যা  

 

(viii) x এর যেকোনো মানের জন্য, $\small (x+5)(x+3)=x^2+8x+15$ −এর সমান চিহ্নের দুপাশে মান সমান হয় । তাই এটি একটি অভেদ ।

উত্তর:   সত্য  

 

 

3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন:  2 × 6 = 12

(i) গণিতের ভাষায় সমস্যাটি হলো

সময় (মিনিট)	দূরত্ব (মিটার)
1	150
25	x

গতিবেগ একই থাকলে সময় ও দূরত্বের সমানুপাতি সম্পর্কের সাহায্যে x -এর মান নির্ণয় করো |

উত্তর:

1 মিনিটে দূরত্ব অতিক্রান্ত হয় 150 মিটার

25 মিনিটে দূরত্ব অতিক্রান্ত হয় $\small 150 \times 25 = 3750$ মিটার

∴ 25 মিনিটে দূরত্ব অতিক্রান্ত হয় 3750 মিটার বা 3.75 কিলোমিটার | (উত্তর)

(ii)

বছর	2009	2010
পড়ার বই	1200	800
গল্পের বই	1400	1100

তালিকাটির সাহায্যে একটি দ্বিস্তম্ভ লেখচিত্র অঙ্কন করো |

সমাধান:

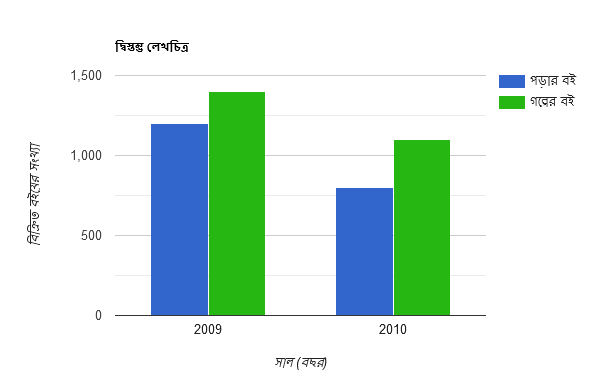
(iii) $\small m+\frac{1}{m}=-P$ হলে, দেখাও যে, $\small m^2+\frac{1}{m^2}=P^2-2$

উত্তর: $\small m+\frac{1}{m}=-P$

উভয়পক্ষে বর্গ করে পাই, 

$\small (m+\frac{1}{m})^2=(-P)^2$ 

বা, $\small (m+\frac{1}{m})^2=P^2$  

বা, $\small m^2+\frac{1}{m^2}+2 \cdot \not{m} \cdot \frac{1}{\not{m}} = P^2$

বা, $\small m^2+\frac{1}{m^2}+2=P^2$

∴ $\small m^2+\frac{1}{m^2}=P^{2}-2$ (প্রমাণিত)

 

(iv) $\small \sqrt 2$ এর দুই দশমিক পর্যন্ত আসন্ন মান নির্ণয় করো ।

উত্তর: 

1 ) 2.0000 ( 1.414
     1____

24)100(

       96

  281)400(

          281

2824)11900(

           11296

               604

∴ $\small \sqrt 2 =1.414 $

∴ $\small \sqrt 2 =1.41$ (দুই দশমিক স্থান পর্যন্ত আসন্নমান) (উত্তর)

 

 

(v) ত্রিভুজের সর্বসমতার শর্তগুলি লেখো ।

উত্তর: ত্রিভুজের সর্বসমতার শর্তগুলি হলো :

1. বাহু-বাহু-বাহু বা S-S-S
2. বাহু-কোণ-বাহু বা S-A-S
3. কোণ-কোণ-বাহু বা A-A-S
4. সমকোণ-অতিভুজ-বাহু বা R-H-S
   

(vi) $\small x+y=5$ এবং $\small x-y=1$ হলে, $\small 8xy(x^2+y^2)$ এর মান নির্ণয় করো । 

উত্তর:$\small 8xy(x^2+y^2)$

$\small = 4xy \space \cdot \space 2(x^2+y^2)$

$\small =\left \{\left (x+y \right )^{2}-\left ( x-y \right )^{2} \right \} \space \cdot \space \left \{\left (x+y \right )^{2}+\left ( x-y \right )^{2} \right \} $

$\small =\left \{\left (5 \right )^{2}-\left ( 1 \right )^{2} \right \} \space \cdot \space \left \{\left (5 \right )^{2}+\left ( 1 \right )^{2} \right \}$

$\small =\left \{ 25-1 \right \} \space \cdot \space \left \{ 25+1 \right \}$

$\small =24 \space \cdot \space 26$

$\small = 624$ (উত্তর)

4. (i) সংখ্যারেখায় (6) + (−2) কে দেখাও |

উত্তর: এটিকে সংখ্যারেখায় উপস্থাপন করলে হবে :

 

(ii) প্রথম বীজগাণিতিক সংখ্যামালাকে দ্বিতীয় সংখ্যামালা দিয়ে ভাগ করে ভাগফল নির্ণয় করো :

$\small 14x^{4}y^{6} - 21x^{3}y^{5}$ ,  $\small -7x^{3}y^{4}$ , যেখানে x ≠ 0, y ≠ 0

উত্তর: 

5. (i) ABC একটি ত্রিভুজ আঁকো যার BC = 5.5 সেমি,  $\small \angle ABC= 60^{o}$ ও$\small \angle ACB= 30^{\circ}$ ।  5

উত্তর:

(ii) করিমচাচার আয়তক্ষেত্রাকার জমির দৈর্ঘ্য প্রস্থের 2 গুণ এবং এই জমির ক্ষেত্রফল 578 বর্গমিটার। করিমচাচার জমিটির দৈর্ঘ্য, প্রস্থ ও পরিসীমা নির্ণয় করো |

উত্তর:  ধরি, আয়তক্ষেত্রাকার জমির প্রস্থ $\small =x$ মিটার.

∴ জমিটির দৈর্ঘ্য $\small =2x$ মিটার.

∴ জমিটির ক্ষেত্রফল $\small = 2x \times x = 2x^{2}$ বর্গমিটার.

প্রশ্নানুসারে,  জমিটির ক্ষেত্রফল = 578 বর্গমিটার

বা, $\small 2x^{2} = 578$

বা, $\small x^{2} = \frac{\mathop{\overset{289}{\not{5}\not{7}\not{8}}}}{\not{2}}$

বা, $\small x^{2} = 289$

বা, $\small x = \sqrt{289}$

∴ $\small x = 17$

∴ আয়তক্ষেত্রাকার জমিটির প্রস্থ = 17 মিটার (উত্তর) 

 

∴ আয়তক্ষেত্রাকার জমিটির দৈর্ঘ্য = 2 ✖17 = 34 মিটার (উত্তর) 

 

∴ আয়তক্ষেত্রাকার জমিটির পরিসীমা = 2 ✖ (দৈর্ঘ্য + প্রস্থ) মিটার

$\small = 2 \times (34+17)$ মিটার

$\small = 2 \times 51$ মিটার

= 102 মিটার (উত্তর) 

(iii) 90 মিটার লম্বা একটি রেলগাড়ি একটি স্তম্ভকে 25 সেকেন্ডে অতিক্রম করলো। রেলগাড়ি গতিবেগ ঘন্টায় কত কিলোমিটার নির্ণয় করো ।   5

উত্তর: 1 ঘন্টা= 3600 সেকেন্ড 

1000 মিটার = 1 কিমি. 

গণিতের ভাষায় সমস্যাটি হলো :

সময় (সেকেন্ড)          দূরত্ব (মিটার)

      25                          90

    3600                          ?

সময় বাড়লে একই সময়ে ট্রেনটি বেশি দূরত্ব অতিক্রম করবে |

তাই, সময় ও দূরত্বের মধ্যে সরল সম্পর্ক |

∴ সমানুপাতটি হবে, 25 : 3600  : :  90 : *

 

∴ নির্ণেয় দূরত্ব $\small  \frac{\overset{144}{\not{3}\not{6}\not{0}\not{0}} \times 90}{\not{2}\not{5}} = 12960$ মিটার = 12.96 কিমি.

∴ রেলগাড়িটি 3600 সেকেন্ড অর্থাৎ 1 ঘন্টায় 12.96 কিমি. দূরত্ব অতিক্রম করে |

∴ রেলগাড়িটির গতিবেগ 12.96 কিমি./ঘন্টা | (উত্তর)

---

আমাদের দ্বারা প্রকাশিত মডেল টাস্ক এর উত্তরগুলি ভালো লেগে থাকলে আমাদের ফেসবুক পেজ লাইক করে রাখতে পারো এবং আমাদের youtube চ্যানেল সাবস্ক্রাইব করে রাখতে পারো | নিচে দেওয়া লিংক থেকে Facebook YouTube জয়েন করো |

• Esho Seekhi Facebok
• Esho Seekhi YouTube

  

এছাড়া তোমাদের আরও কোনো প্রশ্ন থাকলে নিচে কমেন্ট করে আমাদের জানাতে পারো অথবা আমাদের ফেসবুকে অথবা টেলিগ্রামে মেসেজ করতে পারো |

আমাদের টেলিগ্রাম গ্রুপে জয়েন হতে পাশের লিঙ্কে ক্লিক করুন : Telegram

এছাড়া আমাদের ফেসবুক পেজেও প্রশ্নের ছবি তুলে পাঠাতে পারো | আমাদের ফেসবুক পেজ জয়েন করার জন্য পাশের লিংকটিতে ক্লিক করো 👉 Esho Seekhi Facebook

Tags:  WBBSE Class 7 Math Model Activity Task Compilation Part 7 Answers 2021, Model Activity Task Solutions Mathematics Part 8 Solutions 2021, Class 7 Mathematics Model Activity Task Compilation, class 7 model activity task part 8 solutions, Model Activity Task Class 7 Math PART 8, WBBSE Class 7 Mathematics Model Activity Task 2021 Answers, wbbse class 7 math model activity task part 8, সপ্তম  শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক 2021 সমাধান পার্ট 8