[FINAL] WBBSE Class 8 Math Model Activity Compilation Part 8 Answers | অষ্টম শ্রেণী গণিত মডেল অ্যাক্টিভিটি পার্ট 8 সমাধান

প্রিয় ছাত্রছাত্রীরা, এসো শিখিতে তোমাদের স্বাগত জানাই | আজকের এই পোস্টে আমরা আলোচনা করব পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের তরফ থেকে দেওয়া অষ্টম শ্রেনীর গণিত এর 2021 এর মডেল অ্যাক্টিভিটি টাস্ক  Compilation এর উত্তরগুলি | আশা করি এতে তোমরা উপকৃত হবে | ( Class 8 Model Activity Task Compilation Mathematics 2021 PART 8 Solutions)

Class 8

MODEL ACTIVITY COMPILATION

FINAL

গণিত

পূর্ণমান = 50

1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs):

(i) দুটি পরস্পরছেদী সরলরেখার একজোড়া বিপ্রতীপ কোণ পরস্পর পুরক কোণ হলে, অপর জোড়া বিপ্রতীপ কোণ দুটির প্রত্যেকটির মান হবে 

(a) 180°

(b) 45°

(c) 90°

(d) 135°

উত্তর: (d) 135°

(ii) দূরত্ব স্থির থাকলে যদি গতিবেগ দ্বিগুণ হয় তাহলে সময়

(a) অর্ধেক হবে

(b) দ্বিগুণ হবে।

(c) অপরিবর্তিত থাকবে

(d) তিনগুণ হবে।

উত্তর: (a) অর্ধেক হবে |
 

(iii) 20 জন একটি কাজ 8 দিনে করে । 10 জন ওই কাজের $\small \frac{1}{2}$ অংশ করবে |

(a) 32 দিনে

(b) 8 দিনে

(c) 10 দিনে

(d) 2 দিনে

উত্তর: (b) 8 দিনে

 

(iv) এক ধরনের পিতলে তামা ও দস্তার পরিমাণের অনুপাত 5:2, এই ধরনের 28 কিগ্ৰা পিতলে তামা আছে

(a) 8 কিগ্রা.  (b) 11.2 কিগ্রা.   (c) 16.8 কিগ্রা.  (d) 20 কিগ্রা.

উত্তর: (d) 20 কিগ্ৰা 

ব্যাখ্যা : তামার আনুপাতিক ভাগহার = $\small \frac{5}{5+2} = \frac{5}{7}$

 

∴ 28 কিগ্রা পিতলে তামা আছে $\small = \frac{5}{\not{7}} \times \overset{4} {\not{2}\not{8}} = 20$ কিগ্রা.

 

(v) বুলু ও তথাগত একটি কাজ একা একা যথাক্রমে 20 দিনে ও 30 দিনে করতে পারে। দুজনে একসঙ্গে 1 দিনে করে 

উত্তর: (c) $\small (\frac {1}{20}+\frac {1}{30})$ অংশ 

 

(vi) 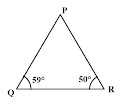চিত্রে,

(a) QR < PR  (b) PR < PQ   (c) QR < PQ  (d) QR > PQ

উত্তর: (d) QR > PQ

ব্যাখ্যা : প্রশ্নানুসারে, $\small \angle PQR = 59^{\circ}$ এবং $\angle PRQ = 50^{\circ}$

∴ $\small \angle RPQ = 180^{\circ} - (59^{\circ} + 50^{\circ})$

$\small = 180^{\circ} - 109^{\circ} = 71^{\circ}$

আমরা জানি, কোনো ত্রিভুজের বৃহত্তর কোণের বিপরীত বাহুর দৈর্ঘ্য সর্বদা ক্ষুদ্রতম কোণের বিপরীত বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর হয় | 

∴ $\small \angle RPQ$ এর বিপরীত বাহুর দৈর্ঘ্য অর্থাৎ, QR এর দৈর্ঘ্য বেশি হবে |

∴ সঠিক উত্তর (d) QR > PQ

(vii) (2m+5n)(2m-5n) এবং mn(2m-5n) সংখ্যামালা দুটির গ.সা.গু. হলো :

(a) 1  (b) mn(2m+5n)(2m-5n)   (c) (2m+5n)  (d) (2m-5n)

উত্তর: (d) (2m-5n)

 

 

2. সত্য / মিথ্যা লেখো (T/F) :

(i) 30 লিটার ডেটল-জলে জল ও ডেটলের পরিমানের অনুপাত 5:1,ইহাতে ডেটল আছে 25 লিটার ।

উত্তর:   মিথ্যা  

ব্যাখ্যা : জল ও ডেটলের পরিমানের অনুপাত 5:1

∴ ডেটলের আনুপাতিক ভাগহার $\small \frac{1}{5+1} = \frac{1}{6}$

30 লিটার ডেটল-জলে ডেটলের পরিমাণ $\small 30 \times \frac{1}{6} = 5$ লিটার

 

(ii) $\small (27x^{3} -343y^{3})$ সংখ্যামালাটি $\small (3x-7y)$ দ্বারা বিভাজ্য।

উত্তর:   সত্য   

(iii)$\small 2a^2b$ এবং $\small 4ab^2$ এর গ.সা.গু হলো $\small 4a^2b^2$ ।

উত্তর:   মিথ্যা  

 

(iv) $\small \frac{x^2}{a}+\frac{a^2}{x}=\frac{x^2+a^2}{a+x}$

উত্তর:  মিথ্যা  

সঠিক উত্তর: $\small \frac{x^2}{a}+\frac{a^2}{x}= \frac{x^3 + a^3}{ax}$

 

(v) চিত্রে $\small x^{\circ}=70^{\circ}-50^{\circ}$

উত্তর:  মিথ্যা  

ব্যাখ্যা : আমরা জানি যে, ত্রিভুজের কোনো একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোন উৎপন্ন হয় সেটির পরিমান অন্তঃস্থ বিপরীত কোন দুটির পরিমাপের যোগফলের সমান ।

∴ উপরোক্ত উপপাদ্য অনুযায়ী, x° = 70° + 50° সঠিক উত্তর |

(vi) হারুন চাচা 1 দিনে কোনো কাজের $\small \frac{1}{10}$ অংশ করেন । সম্পূর্ণ কাজটি করতে হারুনচাচার 10 দিন সময় লাগবে।

উত্তর:   সত্য   

(vii) 2.25 টাকা, 5 টাকার শতকরা 4.5

উত্তর:  মিথ্যা  

ব্যাখ্যা : $\small \left (\frac{2.25}{\not{5}}\times \overset{20}{\not{1}\not{0}\not{0}}  \right )% = 45%$

∴2.25 টাকা, 5 টাকার শতকরা 45 | (সঠিক উত্তর)

 

3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন :

(i) 

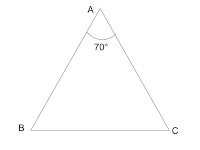
চিত্রে $\small \Delta ABC$ এর $\small AB=AC$ এবং $\small \angle BAC=70^{\circ}$। $\small \angle ABC$ এবং $\small \angle ACB$ এর পরিমাপ নির্ণয় করো । 

উত্তর: প্রশ্নে দেওয়া ত্রিভুজটি হল একটি সমদ্বিবাহু ত্রিভুজ ।

আমরা জানি, সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের সংলগ্ন কোণ দুটির মান সমান দুটি বাহু ও বিষম বাহুর মধ্যবর্তী কোণ দুটিকে নির্দেশ করে তাদের পরিমাপ সমান ।

∵ চিত্রে AB = AC 

∴ $\small \angle ABC = \angle ACB$

ত্রিভুজের তিনটি কোণের সমষ্টি হল $\small 180^{\circ}$

$\small \angle ABC + \angle ACB + \angle BAC=180^{\circ}$ 

বা, $\small \angle ABC + \angle ABC + \angle BAC=180^{\circ}$ [$\small \because \angle ABC = \angle ACB$]

বা, $\small 2\angle ABC + 70^{\circ}=180^{\circ}$

বা, $\small 2\angle ABC =110^{\circ}$

বা, $\small \angle ABC=55^{\circ}$

∴ $\small \angle ABC = \angle ACB = 55^{\circ}$  (উত্তর)

 

(ii) দুটি সমান মাপের কৌটায় মিশ্র চায়ের আসাম চা ও দার্জিলিং চায়ের পরিমাণের অনুপাত 5:18 এবং 2:3 । কোন কৌটায় আসাম চায়ের পরিমাণ বেশী আছে ?

উত্তর: প্রথম কৌটায় আসাম চা : দার্জিলিং চা = 5 : 18

দ্বিতীয় কৌটায় আসাম চা : দার্জিলিং চা = 2 : 3

∴ প্রথম কৌটায় আসাম চায়ের আনুপাতিক ভাগহার $\small \frac{5}{5+18} = \frac{5}{23}$

দ্বিতীয় কৌটায় আসাম চায়ের আনুপাতিক ভাগহার $\small \frac{2}{2 + 3} = \frac{2}{5}$

∴ তুলনা করে পাই, 

প্রথম কৌটা 

$\small =\frac{5}{23} = \frac{5 \times 5}{23 \times 5} = \frac{25}{115}$ 

দ্বিতীয় কৌটা 

$\small =\frac{2}{5} = \frac{2 \times 23}{5 \times 23} = \frac{46}{115}$ 

∵ 46 > 25

∴ দ্বিতীয় কৌটায় অসম চা য়ের পরিমাণ বেশী | (উত্তর) 

 

(iii) গণিতের ভাষায় সমস্যাটি হল 

(a) সময় স্থির থাকলে গোরুর সংখ্যার সঙ্গে খড়ের পরিমাণের সমানুপাত সম্পর্কটি লেখো ।

উত্তর: একই সময়ে গরুর সংখ্যা বাড়লে খড়ের পরিমাণ বাড়বে এবং গরুর সংখ্যা কমলে খড়ের পরিমাণ কমবে |

∴ সময় স্থির থাকলে গরুর সংখ্যার সাথে খড়ের পরিমাণের সরল সম্পর্ক |

(b) গোরুর সংখ্যা স্থির থাকলে সময়ের সঙ্গে খড়ের পরিমাণের সমানুপাত সম্পর্কটি লেখো ।

উত্তর: গরুর সংখ্যা একই থাকলে সময় বাড়লে খড়ের পরিমাণ বাড়বে এবং সময় কমলে খড়ের পরিমাণ কমবে |

∴ গরুর সংখ্যা স্থির থাকলে সময়ের সাথে খড়ের পরিমাণের সরল সম্পর্ক | 

 

(iv) $\small x^2+px+q$ বীজগাণিতিক সংখ্যামালায় $\small p=a+b$ এবং $q=a\times b$হলে, সংখ্যামালাটির উৎপাদক নির্ণয় করো ।

উত্তর: $\small x^2+px+q$ সন্খ্যামালায় p = a + b এবং q = ab বসিয়ে পাই,

$\small x^2+(a+b)x+ab$

= $\small x^2+ax+bx+ab$

=$\small x(x+a)+b(x+a)$

=$\small (x+a)(x+b)$ (উত্তর)

4.(i) $\small \frac{x}{2}=\frac{1}{2x}+1$ হলে, $\small \left ( x^{3}-\frac{1}{x^{3}} \right )$ এর মান নির্ণয় করো |

সমাধান: $\small \frac{x}{2}=\frac{1}{2x}+1$

 

বা, $\small \frac{x}{2}-\frac{1}{2x}=1$

 

উভয়পক্ষকে 2 দ্বারা গুন করে পাই,

বা, $\small \not{2} \times \frac{x}{\not{2}}-\not{2} \times \frac{1}{\not{2}x}=1$

বা, $\small x-\frac{1}{x}=2$

উভয়পক্ষে ঘন করে পাই,

$\small \left (x-\frac{1}{x}  \right )^{3}=(2)^{3}$

 

বা, $\small (x)^{3}-\left ( \frac{1}{x} \right )^{3}-3\cdot \not{x}\cdot \frac{1}{\not{x}}\left (x-\frac{1}{x}  \right )$

বা, $\small x^{3}-\frac{1}{x^{3}}-3\cdot 1 \cdot 2 = 8$

বা, $\small x^{3}-\frac{1}{x^{3}}-6 = 8$

বা, $\small x^{3}-\frac{1}{x^{3}}= 8+6$

∴ $\small x^{3}-\frac{1}{x^{3}}= 14$ (উত্তর)

 

(ii) ভাগ করো : $\small (m^{2}-5m+6)$ কে, $\small (m-3)$ দিয়ে |

সমাধান: 

$\small (m-3)$ ) $\small m^{2}-5m+6$ ( m − 2

                 $\small m^{2}-3m$

              −      +                                   

                        − 2m + 6

                        − 2m + 6

                         +       −                           

                          0

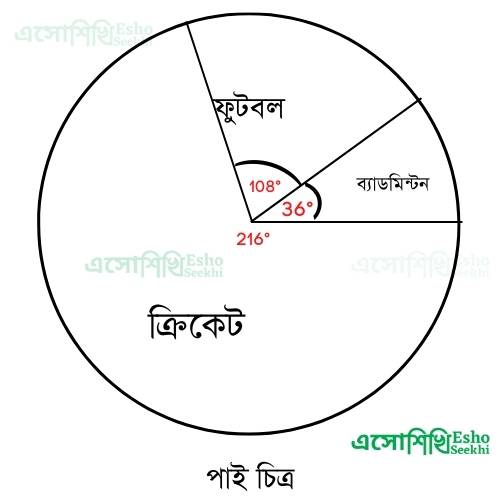
∴ নির্ণেয় ভাগফল = (m − 2) (উত্তর)

5. ক্লাসের ছাত্রছাত্রীরা কোন কোন খেলা কতজন করে পছন্দ করে শতকরায় তার তালিকা হলো  (একজন কেবলমাত্র একটি খেলায় পছন্দ করবে )

খেলা	খেলা পছন্দ করা ছাত্রছাত্রীর সংখ্যা (শতকরায়)
ক্রিকেট	60
ফুটবল	30
ব্যাডমিন্টন	10

পাই চিত্রে, যে বৃত্তকলাগুলি তথ্যটির অংশগুলিকে বোঝাবে সেই বৃত্তকলাগুলির কেন্দ্রীয় কোণগুলি নির্ণয় করো এবং তথ্যটির পাই চিত্র অঙ্কন করো |

সমাধান:

খেলা	খেলা পছন্দ করা ছাত্রছাত্রীর সংখ্যা (শতকরায়)	খেলা পছন্দ করা ছাত্রছাত্রীর সংখ্যা (ভগ্নাংশে)	কেন্দ্রীয় কোণের মান
ক্রিকেট	60	$\small \frac{\overset{3}{\not{6}\not{0}}}{\underset{5}{\not{1}\not{0}\not{0}}} = \frac{3}{5}$	$\small \overset{72}{\not{3} \not{6} \not{0}}\times \frac{3}{\not{5}} = 216^{\circ}$
ফুটবল	30	$\small \frac{3\not{0}}{1\thinspace 0 \thinspace \not{0}} = \frac{3}{10}$	$\small 3\thinspace \thinspace 6\not{0}\times \frac{3}{1\not{0}} = 108^{\circ}$
ব্যাডমিন্টন	10	$\small \frac{1\not{0}}{1\thinspace 0 \thinspace \not{0}} = \frac{1}{10}$	$\small 3\thinspace \thinspace 6\not{0}\times \frac{1}{1\not{0}} = 36^{\circ}$

 

∴ উপরের তথ্য গুলিকে পাই চিত্রের সাহায্যে প্রকাশ করলে হয়,

6.  (i)  যুক্তি দিয়ে প্রমান করো যে, ত্রিভুজের কোনো একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোন উৎপন্ন হয় সেটির পরিমান অন্তঃস্থ বিপরীত কোন দুটির পরিমাপের যোগফলের সমান ।

উত্তর:

(ii) প্রমাণ করো যে, কোনো ত্রিভুজের তিনটি কোণের সমষ্টি 180°

উত্তর : 

 

7.  5 অশ্বক্ষমতা সম্পন্ন একটি পাম্প 36000 লিটার জল 8 ঘন্টায় উপরে তুলতে পারে । 7 অশ্বক্ষমতা সম্পন্ন পাম্পের 63000 লিটার জল তুলতে কত সময় লাগবে ত্রৈরাশিক পদ্ধতিতে নির্ণয় করো |   

উত্তর : গণিতের ভাষায় সমস্যাটি হল,

অশ্বক্ষমতা   জলের পরিমাণ (লি.)   সময় (ঘন্টা)

      5                36000                 8

      7                63000                 ?

(i) অশ্বক্ষমতা স্থির থাকলে, জলের পরিমাণ ও সময়ের মধ্যে সরল সম্পর্ক |

∴ ভগ্নাংশটি হবে $\small \frac{63000}{36000}$ 

(ii) জলের পরিমাণ স্থির থাকলে, অশ্বক্ষমতা ও সময়ের মধ্যে ব্যস্ত সম্পর্ক |

∴ ভগ্নাংশটি হবে $\small \frac{5}{7}$ 

∴ নির্ণেয় সময় $\small \frac{6\thinspace 3\not{0}\not{0}\not{0}}{3\thinspace 6\not{0}\not{0}\not{0}} \times \frac{5}{7} \times 8$

= 10 ঘন্টা (উত্তর)

---

আমাদের দ্বারা প্রকাশিত মডেল টাস্ক এর উত্তরগুলি ভালো লেগে থাকলে আমাদের ফেসবুক পেজ লাইক করে রাখতে পারো এবং আমাদের youtube চ্যানেল সাবস্ক্রাইব করে রাখতে পারো | নিচে দেওয়া লিংক থেকে Facebook YouTube জয়েন করো |

• Esho Seekhi Facebok
• Esho Seekhi YouTube

  

এছাড়া তোমাদের আরও কোনো প্রশ্ন থাকলে নিচে কমেন্ট করে আমাদের জানাতে পারো অথবা আমাদের ফেসবুকে অথবা টেলিগ্রামে মেসেজ করতে পারো |

আমাদের টেলিগ্রাম গ্রুপে জয়েন হতে পাশের লিঙ্কে ক্লিক করুন : Telegram

এছাড়া আমাদের ফেসবুক পেজেও প্রশ্নের ছবি তুলে পাঠাতে পারো | আমাদের ফেসবুক পেজ জয়েন করার জন্য পাশের লিংকটিতে ক্লিক করো 👉 Esho Seekhi Facebook

Tags:  WBBSE Class 8 Mathematics Model Activity Task Compilation Part 8 Final Answers 2021, Model Activity Task Solutions Mathematics Part 8 Solutions 2021, Class 8 Math Model Activity Task Compilation, class 8 model activity task part 8 solutions, Model Activity Task Class 8 Mathematics Final, WBBSE Class 8 Mathematics Model Activity Task 2021 Answers, wbbse class 8 math model activity task part 8, অষ্টম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক 2021 সমাধান পার্ট 8