[PART 5] WBBSE Class 7 Mathematics Model Activity Task Solutions 2021 | সপ্তম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক

প্রিয় ছাত্রছাত্রীরা, এসো শিখিতে তোমাদের স্বাগত জানাই | এবছর আবার দেওয়া হলো বাংলার শিক্ষা পোর্টাল থেকে আবার দেওয়া হলো আগস্ট মাসের বিভিন্ন শ্রেনীর মডেল অ্যাক্টিভিটি টাস্ক |

আজকের এই পোস্টে আমরা আলোচনা করব পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের তরফ থেকে দেওয়া আগস্ট মাসের সপ্তম শ্রেনীর গণিত এর 2021 এর মডেল অ্যাক্টিভিটি টাস্ক এর উত্তরগুলি | আশা করি এতে তোমরা উপকৃত হবে | ( Class 7 Model Activity Task Mathematics 2021 PART 5 [2ND SERIES])

WBBSE Class 7

Model Activity Task 2021 2ND SERIES

MATHEMATICS

PART 5

নীচের প্রশ্নগুলির উত্তর দাও :

1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs)

(i) কোনটি ত্রিভুজের সর্বসমতার শর্ত নয়

(a) বাহু-বাহু-বাহু  (b) বাহু-কোণ-বাহু  (c) কোণ-কোণ-বাহু  (d) কোণ-কোণ-কোণ

উত্তর: (d) কোণ-কোণ-কোণ

(ii)$\small \frac{4}{49}$ বর্গসেমি ক্ষেত্রফল বিশিষ্ট বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য হবে 

 

(a) $\small \sqrt\frac{4}{49}$ (b) $\small \frac{2}{7}$ সেমি. (c) 2 সেমি. (d) 7 সেমি.

উত্তর: (b) $\small \frac{2}{7}$ সেমি.

ব্যাখ্যা: বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য হবে $\small= \sqrt{ \frac{4}{49}}$

(iii) 1.69 এর বর্গমূল হলো

(a) 13 (b) 1.3 (c) 0.13 (d) 13.03

উত্তর: (b) 1.3

ব্যাখ্যা: 1.69 এর বর্গমূল $\small \sqrt{1.69}$

$\small =\sqrt{\frac{169}{100}}$

$\small =\sqrt{\frac{13\times 13}{10\times10}}$

$\small =\frac{13}{10}$

$\small =1.3$

(iv) xy=

(a) $\small (x+y)^{2}-(x-y)^{2}$ (b) $\small (x+y)^{2}+(x-y)^{2}$

(c) $\small (\frac{x+y}{2})^2-(\frac{x-y}{2})^2$ (d) $\small (\frac{x+y}{2})^2+(\frac{x-y}{2})^2$

উত্তর: $\small (\frac{x+y}{2})^2-(\frac{x-y}{2})^2$

2. সত্য / মিথ্যা লেখো(T/F):

(i) $\small (x+y)^2$ এর সূত্র থেকে $\small (x-y)^2$ এর সূত্র নির্ণয় করতে y এর পরিবর্তে (-y) লিখতে হবে।

উত্তর:   সত্য  

(ii) $\small (4-x)(x-4)=16-x^2$

উত্তর:   মিথ্যা  

(iii)

চিত্রে, $\small \angle 1$ ও $\small \angle 2$ পরস্পর অনুরূপ কোণ।

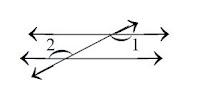
উত্তর:   মিথ্যা  

 

(iv) 

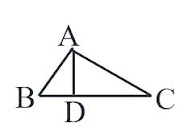
চিত্রে, বিষমবাহু $\small \Delta ABC$ এর একটি উচ্চতা AD। AD ত্রিভুজটির একটি মধ্যমা।

উত্তর:   মিথ্যা  

# মধ্যমা হলো কোনো ত্রিভুজের শীর্ষবিন্দু ও বিপরীত বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাংশ |

3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন:

(i) গণিতের ভাষায় সমস্যাটি হলো

সময় (মিনিট)	দূরত্ব (মিটার)
1	150
25	x

গতিবেগ একই থাকলে সময় ও দূরত্বের সমানুপাতি সম্পর্কের সাহায্যে x -এর মান নির্ণয় করো |

উত্তর:

1 মিনিটে দূরত্ব অতিক্রান্ত হয় 150 মিটার

25 মিনিটে দূরত্ব অতিক্রান্ত হয় $\small 150 \times 25 = 3750$ মিটার

∴ 25 মিনিটে দূরত্ব অতিক্রান্ত হয় 3750 মিটার বা 3.75 কিলোমিটার | (উত্তর)

(ii)

বছর	2009	2010
পড়ার বই	1200	800
গল্পের বই	1400	1100

তালিকাটির সাহায্যে একটি দ্বিস্তম্ভ লেখচিত্র অঙ্কন করো |

সমাধান:

 

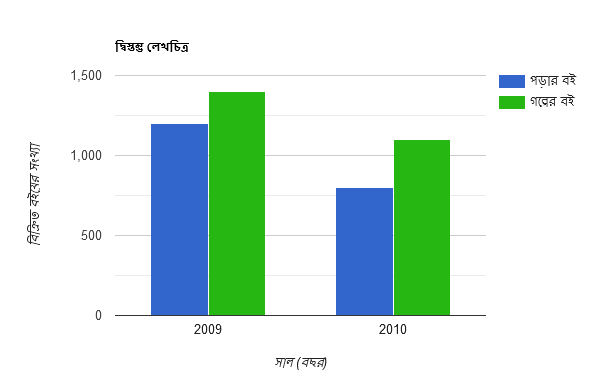
(iii) $\small m+\frac{1}{m}=-P$ হলে, দেখাও যে, $\small m^2+\frac{1}{m^2}=P^2-2$

উত্তর: $\small m+\frac{1}{m}=-P$

উভয়পক্ষে বর্গ করে পাই, 

$\small (m+\frac{1}{m})^2=(-P)^2$ 

বা, $\small (m+\frac{1}{m})^2=P^2$  

বা, $\small m^2+\frac{1}{m^2}+2 \cdot \not{m} \cdot \frac{1}{\not{m}} = P^2$

বা, $\small m^2+\frac{1}{m^2}+2=P^2$

∴ $\small m^2+\frac{1}{m^2}=P^{2}-2$ (প্রমাণিত)

 

4. করিমচাচার আয়তক্ষেত্রাকার জমির দৈর্ঘ্য প্রস্থের 2 গুণ এবং এই জমির ক্ষেত্রফল 578 বর্গমিটার। করিমচাচার জমিটির দৈর্ঘ্য, প্রস্থ ও পরিসীমা নির্ণয় করো |

উত্তর:  ধরি, আয়তক্ষেত্রাকার জমির প্রস্থ $\small =x$ মিটার.

∴ জমিটির দৈর্ঘ্য $\small =2x$ মিটার.

∴ জমিটির ক্ষেত্রফল $\small = 2x \times x = 2x^{2}$ বর্গমিটার.

প্রশ্নানুসারে,  জমিটির ক্ষেত্রফল = 578 বর্গমিটার

বা, $\small 2x^{2} = 578$

বা, $\small x^{2} = \frac{\mathop{\overset{289}{\not{5}\not{7}\not{8}}}}{\not{2}}$

বা, $\small x^{2} = 289$

বা, $\small x = \sqrt{289}$

∴ $\small x = 17$

∴ আয়তক্ষেত্রাকার জমিটির প্রস্থ = 17 মিটার (উত্তর) 

 

∴ আয়তক্ষেত্রাকার জমিটির দৈর্ঘ্য = 2 ✖17 = 34 মিটার (উত্তর) 

 

∴ আয়তক্ষেত্রাকার জমিটির পরিসীমা = 2 ✖ (দৈর্ঘ্য + প্রস্থ) মিটার

$\small = 2 \times (34+17)$ মিটার

$\small = 2 \times 51$ মিটার

= 102 মিটার (উত্তর) 

 

সপ্তমশ্রেনীর অন্যান্য মডেল টাস্ক PART 5 এর সমাধানের লিংক নিচে দেওয়া হলো :

丨সপ্তম শ্রেণী ইংরেজি মডেল অ্যাক্টিভিটি টাস্ক Part 5

丨সপ্তম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক Part 5

丨সপ্তম শ্রেণী ইতিহাস মডেল অ্যাক্টিভিটি টাস্ক Part 5

丨সপ্তম শ্রেণী ভূগোল মডেল অ্যাক্টিভিটি টাস্ক Part 5

丨সপ্তম শ্রেণী বিজ্ঞান মডেল অ্যাক্টিভিটি টাস্ক Part 5

আশা করি তোমরা উত্তরগুলি নিজেদের খাতায় টুকে নিয়েছ | আমাদের দ্বারা প্রকাশিত মডেল টাস্ক এর উত্তরগুলি ভালো লেগেথাকলে আমাদের ফেসবুক পেজ লাইক করে রাখতে পারো এবং আমাদের youtube চ্যানেল সাবস্ক্রাইব করে রাখতে পারো | নিচে দেওয়া লিংক থেকে Facebook YouTube জয়েন করো |

• Esho Seekhi Facebok
• Esho Seekhi YouTube

 

এছাড়া তোমাদের আরও কোনো প্রশ্ন থাকলে নিচে কমেন্ট করে আমাদের জানাতে পারো অথবা আমাদের ফেসবুকে অথবা টেলিগ্রামে মেসেজ করতে পারো |

আমাদের টেলিগ্রাম গ্রুপে জয়েন হতে পাশের লিঙ্কে ক্লিক করুন : Telegram

এছাড়া আমাদের ফেসবুক পেজেও প্রশ্নের ছবি তুলে পাঠাতে পারো | আমাদের ফেসবুক পেজ জয়েন করার জন্য পাশের লিংকটিতে ক্লিক করো 👉 Esho Seekhi Facebook

 

Tags: model activity task 2021 class 7 all subject second series, class 7 model activity task 2021, model activity task class 7 mathematics 2021, model activity task class 7 mathematics part 5 answers, model activity task class 7 mathematics 2nd series, model activity task class 7 mathematics part 5 answers, WBBSE Class 7 Mathematics Model Activity Task Answers, Class 7 Model Activity Task Answers Mathematics, সপ্তম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক উত্তরমালা 2021 পার্ট 5

© Esho Seekhi Online Education Platform