প্রিয় ছাত্রছাত্রীরা, এসো শিখিতে তোমাদের স্বাগত জানাই | আজকের
এই পোস্টে আমরা আলোচনা করব পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের তরফ থেকে দেওয়া নবম শ্রেনীর গণিত এর 2021 এর মডেল অ্যাক্টিভিটি টাস্ক Compilation এর
উত্তরগুলি | আশা করি এতে তোমরা উপকৃত হবে | ( Class 9 Model Activity Task Compilation Math 2021 PART 8 Solutions)
নবম শ্রেণী
MODEL ACTIVITY COMPILATION
গণিত
নীচের প্রশ্নগুলির উত্তর লেখো :
1. বহুমুখী উত্তরধর্মী প্রশ্ন: (MCQs)
(i) একজন সবজি বিক্রেতা 20 টাকায় 10 টি লেবু কিনে 20 টাকায় 8টি লেবু বিক্রি করেন, তার শতকরা লাভ হয়
উত্তর: (a) 25
(ii) PQRS ট্রাপিজিয়ামের দুটি তির্যক বাহু PS ও QR এর মধ্যবিন্দু যথাক্রমে X ও Y , তবে XY=
উত্তর: (c) $\small \frac{1}{2}$(PQ+RS)
(iii) 105-140 শ্রেণীটির পরিসংখ্যা হলে, শ্রেণীটির পরিসংখ্যার ঘনত্ব হবে
উত্তর: (b) 0.4
(iv) 3 মিটার লম্বা ও 2 মিটার চওড়া একটি আয়তকার জায়গা 5 ডেসি.মি বর্গ টালি দিয়ে বাঁধতে হলে টালি লাগবে
উত্তর: (c) 24টি
(v) শতকরা লাভ 10 হলে, ক্রয় মূল্য ও বিক্রয় মূল্যের অনুপাত হবে
উত্তর: (c) 10:11
(vi) $\small \Delta ABC$-এর বাহুর মধ্যবিন্দু D দিয়ে সমান্তরাল টানা হলো যা AC বাহুকে E বিন্দুতে ছেদ করলো, তাহলে
উত্তর: (b) $\small AE=\frac{1}{2} AC$
(vii) যে অর্ধবৃত্তাকার চাকতির ব্যাসার্ধের 10.5 দৈর্ঘ্য সেমি তার পরিসীমা হলো
উত্তর: (b) $\small (\pi +2) \times 10.5$ সেমি
(viii) যে বর্গাকার চিত্রে কর্ণের দৈর্ঘ্য $\small 13\sqrt 2$ সেমি, তার একটি বাহুর দৈর্ঘ্য
উত্তর: (d) 13 সেমি
2. সত্য / মিথ্যা লেখো(T/F):
(i) ABC সমকোণী ত্রিভুজের $\small \angle BAC=90^{o}$ এবং BC এর মধ্যবিন্দু D হলে, $\small AD=\frac{1}{2} BC$ |
উত্তর: সত্য
(ii) একটি পরিসংখ্যা বিভাজন তালিকায় একটি শ্রেণির মধ্যবিন্দু 10 এবং প্রতিটি শ্রেণির দৈর্ঘ্য 6 হলে শ্রেণিটির নিম্নসীমা হবে 8 |
উত্তর: মিথ্যা
(iii) একটি সামন্তরিক আকারের ক্ষেত্র, একটি আয়তক্ষেত্র এবং একটি ত্রিভুজাকার ক্ষেত্র একই ভূমি একই সমান্তরাল সরলরেখা যুগলের মধ্যে অবস্থিত এবং তাদের ক্ষেত্রফল যথাক্রমে P,RওT হলে $\small P=R=\frac{T}{2}$ হবে ।
উত্তর: মিথ্যা
(iv) একটি সমবাহু ত্রিভুজের ক্ষেত্রফল ও উচ্চতার সংখ্যমান সমান হলে, ত্রিভুজটির বাহুর দৈর্ঘ্য হবে 1 একক ।
উত্তর: মিথ্যা
(v) ধার্যমূল্যের উপর ছাড় নির্ভর করে।
উত্তর: সত্য
(vi) পরিসংখ্যা বহুভুজ অঙ্কনের জন্য প্রথম শ্রেণীর ঠিক আগের একটি পরিসংখ্যা হবে '0'
উত্তর: সত্য
(vii)
চিত্রে, ABCD বর্গক্ষেত্রের ক্ষেত্রফল ABEF রম্বস আঁকার ক্ষেত্রে ক্ষেত্রফল সমান হবে ।
উত্তর: মিথ্যা
সঠিক উত্তর : ABCD বর্গক্ষেত্রের ক্ষেত্রফল, ABEF বর্গক্ষেত্রের ক্ষেত্রফলের থেকে বেশি হবে |
(viii) প্রতিটি বৃত্তের পরিধি ও ব্যাসের দৈর্ঘের অনুপাত একটি নির্দিষ্ট সংখ্যা
উত্তর: সত্য
ব্যাখ্যা :কোনো বৃত্তের ব্যাসার্ধ r হলে, সেই বৃত্তটির
পরিধি = 2𝝅r এবং ব্যাস = 2r
∴ বৃত্তের পরিধি : বৃত্তের ব্যাস
= 2𝝅r : 2r
= 𝝅 : 1
অর্থাৎ, বৃত্তের পরিধি ও ব্যাসের দৈর্ঘের অনুপাত সর্বদা 𝝅 হবে যা একটি নির্দিষ্ট সংখ্যা |
 |
| বিভিন্ন প্রশ্নোত্তরের আলোচনার জন্য আমাদের টেলিগ্রাম গ্রুপ জয়েন করুন |
3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন : 2 × 7 = 14
(i) $\small g(x)=2x-16$ বহুপদী সংখ্যামলার সমীকরণটি লেখো এবং বহুপদী সংখ্যামালাটির শূন্য নির্ণয় করো ।
সমাধান: $\small g(x)=2x-16$ বহুপদী সংখ্যামলার সমীকরণটি হবে :
g(x) = 0
বা, $\small 2x-16=0$
বা, $\small 2x=16$
বা, $\small x=\frac{16}{2}$
∴ $\small x = 8$
∴ $\small x = 8$ এই মানের জন্য g(x) এর মান 0 হবে |
∴ বহুপদী সংখ্যামালাটির শূন্য হলো 8 (উত্তর)
(ii) $\small (8x^3+8x-5)$ বহুপদী সংখ্যামলার একটি উৎপাদক নির্ণয় করো।
সমাধান: ধরি, $\small f(x)= (8x^3+8x-5)$
এখন $\small x=\frac{1}{2}$ হলে,
$\small f(x)= (8x^3+8x-5)$
$\small =\left \{ 8\times \left (\frac{1}{2} \right )^3+8\times \left (\frac{1}{2} \right )-5\right \}$
$\small =\left \{ \not{8}\times \frac{1}{\not{8}}+\overset{4}{\not{8}}\times \left (\frac{1}{\not{2}} \right )-5\right \}$
$\small = \left \{ 1+4-5 \right \} = 0$
∴ বহুপদী সংখ্যামলাটির একটি উৎপাদক হবে $\small x=\frac{1}{2}$
বা, $\small 2x=1$
∴ $\small 2x-1=0$ (উত্তর)
(iii) (-2,2) এবং (4,6) বিন্দু দুটির মধ্যে দূরত্ব নির্ণয় করো ।
সমাধান: ধরি, বিন্দু দুটি হল P(-2,-2) এবং Q(4,6)
∴ P ও Q বিন্দু দুটির মধ্যে দূরত্ব হবে,
$\small \overline{PQ}=\sqrt{(x_1-x_2)^{2}+(y_1-y_2)^{2}}$ একক
$\small =\sqrt{(-2-4)^{2}+(-2-6)^{2}}$ একক
$\small =\sqrt{(-6)^{2}+(-8)^{2}}$ একক
$\small =\sqrt{36+64}$ একক
$\small =\sqrt{100}$ একক
$\small =10$ একক
(iv) একটি ঘড়ি পরপর 10% ও 5% ছাড়ে বিক্রয় করা হলে সমতুল্য ছাড় কত হবে ?
উত্তর: ধরি, ঘড়িটির ধার্য্য মূল্য = 100 টাকা
10% ছাড় দিলে ছাড়ের পরিমাণ হবে = 10 টাকা
∴ প্রথম ছাড়ের ঘড়িটির মূল্য হয় = (100 - 10) = 90 টাকা
দ্বিতীয় বার ছাড় দেওয়া হবে এই 90 টাকার ওপর |
∴ 90 টাকার ওপর 5% ছাড় দিলে ছাড়ের পরিমাণ হবে $\small = 90\times 5%$
$\small =9\not{0}\times \frac{\not{5}}{\underset{2}{\not{1}\not{0}\not{0}}}$
$\small =\frac{9}{2} = 4.5$ টাকা
সর্বমোট ছাড়ের পরিমাণ = 10 টাকা + 4.5 টাকা = 14.5 টাকা
সমতুল্য ছাড় = $\small \frac{14.5}{100} \times 100$ % = 14.5%
(v) একটি বৃত্তের ব্যাসের দৈর্ঘ্য এবং একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য সমান হলে, তাদের পরিসীমার অনুপাত কত হবে ?
উত্তর: ধরি, বৃত্তের ব্যাসের দৈর্ঘ্য $\small = 2a$ একক
∴ বৃত্তের ব্যাসার্ধ $\small = \frac{2a}{2} = a$ একক
∴ বৃত্তের পরিসীমা বা পরিধি $\small =2\pi a$ একক
আবার, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য $\small = 2a$ একক
∴ বর্গক্ষেত্রের পরিসীমা = 4 ⤬ বাহুর দৈর্ঘ্য
$\small 4 \times 2a = 8a$ একক
∴ বৃত্তের পরিসীমা : বর্গক্ষেত্রের পরিসীমা
$\small 2\pi a : 8a$
$\small = \pi : 4$
পাই ($\small \pi$)- এর মান $\small \frac{22}{7}$ বসালে অনুপাতটি হবে,
$\small \frac{22}{7} : 4$
$\small = 22 : 28$
$\small = 11 : 14$ (উত্তর)
(vi) 10 টি পেনের ক্রয়মূল্য 8টি পেনের বিক্রয়মূল্যের সমান হলে, শতকরা লাভ কত ?
উত্তর: ধরি, 10 টি পেনের ক্রয়মূল্য = 100 টাকা
∴ 8 টি পেনের বিক্রয়মূল্য = 100 টাকা
1 টি পেনের বিক্রয়মূল্য = $\small \frac{100}{8}$ টাকা
10 টি পেনের বিক্রয়মূল্য = $\small \frac{100}{8} \times 10$ টাকা = 125 টাকা
∴ 10 টি পেন বিক্রয় করে মোট লাভ = (125 − 100) = 25 টাকা
∴ শতকরা লাভ = $\small (\frac{25}{100} \times 100)$
= $\small 25$ (উত্তর)
(vii) 
চিত্রে, ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 96 বর্গমি. এবং ভূমি BC = 20 মি. হলে, ত্রিভুজটির উচ্চতা h মি. নির্ণয় করো ।
উত্তর: আমরা জানি,
ত্রিভুজের ক্ষেত্রফল = $\small \frac {1}{2}\times $ ভূমি $\small \times$ উচ্চতা
বা, $\small 96 = \frac{1}{2}\times 20 \times h$
বা, $\small 96 \times \not{2} \times \frac{1}{\underset{10}{\not{2}\not{0}}}= h$
বা, $\small \frac{96}{10}= h$
বা, $\small 9.6= h$
∴ h = 9.6
∴ ত্রিভুজটির উচ্চতা 9.6 মিটার | (উত্তর)
4.
(i) যুক্তি দিয়ে প্রমান করো, যে কোনো চতুর্ভুজের একজোড়া বিপরীত বাহু সমান ও সমান্তরাল হলে, চতুর্ভুজ সামন্তরিক হবে ।
(ii) যুক্তি দিয়ে প্রমান করো যে, কোনো ত্রিভুজের দুটি বাহুর মধ্যবিন্দুদ্বয়ের সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক ।
উত্তর:
(iii) সমদ্বিবাহু ত্রিভুজ অঙ্কন করো যার সমান বাহু দুটির প্রত্যেকটির দৈর্ঘ্য 8 সেমি এবং সমান বাহু দুটির অন্তর্ভুক্ত $\small 30^{\circ}$ কোণ ওই ত্রিভুজটির সমান ক্ষেত্রফল বিশিষ্ট একটি আয়তক্ষেত্র অঙ্কন করো । 5
উত্তর:
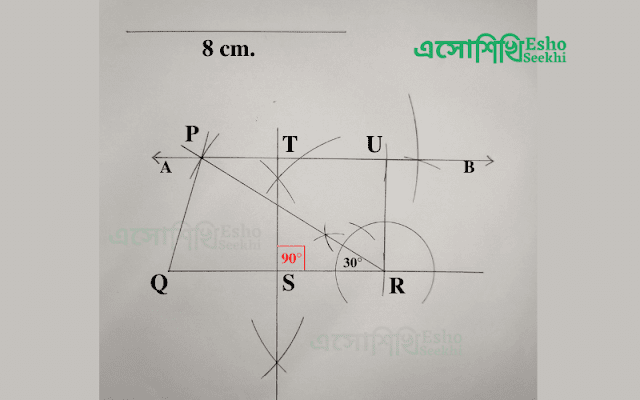
PQR একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করলাম যার সমান বাহু দুটি হলো PR = QR = 8 সেমি. এবং সমান বাহু দুটির অন্তর্ভুক্ত কোণ $\small \angle SRU = 30^{\circ}$ | এই PQR সমদ্বিবাহু ত্রিভুজের সমান ক্ষেত্রফলবিশিষ্ট একটি আয়তক্ষেত্র RSTU অঙ্কন করা হলো |
(iv) নীচের পরিসংখ্যা বিভাজন ছকটির পরিসংখ্যা বহুভুজ অঙ্কন করো । 5
উত্তর:
x- অক্ষ বরাবর ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের 2 টি বাহুর দৈর্ঘ্য = 1 একক এবং y-অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 2 টি বাহুর দৈর্ঘ্য = 1 একক ধরে ছক কাগজে X ও Y দুটি লম্ব অক্ষ অঙ্কন করা হলো |
প্রত্যেকটি শ্রেণির শ্রেণি-মধ্যক ভুজ এবং শ্রেণি পরিসংখ্যাকে কোটি ধরে ছক কাগজে (-2.5, 0); (2.5, 4); (7.5, 10); (12.5, 24); (17.5, 12); (22.5, 20); (27.5, 8); (32.5, 0) বিন্দুগুলি স্থাপন করলাম | এবপর ওই বিন্দুগুলিকে পরপর সরলরেখাংশ দ্বারা যোগ করে ABCDEFGH পরিসংখ্যা বহুভুজটি অঙ্কন করা হলো |
উপরের গ্রাফটি বুঝতে অসুবিধে হলে নীচের দেওয়া লিংক থেকে গ্রাফটির PDF Download করুন
CLASS 9 Part 8 All Links
Part 8 (Final)丨English Model Activity Task
Part 8 (Final)丨ভৌতবিজ্ঞান মডেল টাস্ক (Physical Science)
Part 8 (Final)丨জীবন বিজ্ঞান মডেল টাস্ক (Life Science)
Part 8 (Final)丨গণিত মডেল অ্যাক্টিভিটি টাস্ক (Math)
Part 8 (Final)丨ইতিহাস মডেল অ্যাক্টিভিটি টাস্ক
Part 8 (Final)丨ভূগোল মডেল অ্যাক্টিভিটি টাস্কআমাদের দ্বারা প্রকাশিত মডেল টাস্ক এর উত্তরগুলি ভালো লেগেথাকলে আমাদের ফেসবুক পেজ লাইক করে রাখতে পারো এবং আমাদের youtube চ্যানেল সাবস্ক্রাইব করে রাখতে পারো | নিচে দেওয়া লিংক থেকে Facebook YouTube জয়েন করো |
এছাড়া তোমাদের আরও কোনো প্রশ্ন থাকলে নিচে কমেন্ট করে আমাদের জানাতে পারো অথবা আমাদের ফেসবুকে অথবা টেলিগ্রামে মেসেজ করতে পারো |
আমাদের টেলিগ্রাম গ্রুপে জয়েন হতে পাশের লিঙ্কে ক্লিক করুন : Telegram
এছাড়া আমাদের ফেসবুক পেজেও প্রশ্নের ছবি তুলে পাঠাতে পারো | আমাদের ফেসবুক পেজ জয়েন করার জন্য পাশের লিংকটিতে ক্লিক করো 👉 Esho Seekhi FacebookTags: WBBSE Class 9 Mathematics Model Activity Task Compilation Part 8 Answers 2021, Model Activity Task Solutions Mathematics Part 8 Solutions 2021, Class 9 Math Model Activity Task Compilation, class 9 model activity task part 8 solutions, Model Activity Task Class 9 Mathematics PART 8, WBBSE Class 9 Math Model Activity Task 2021 Answers, wbbse class 9 mathematics model activity task part 8, দশম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক 2021 সমাধান পার্ট 8
Post a Comment
Please give your valuable comments. It helps us to improve our content.